江苏省药理学会
传说古希腊哲学大师苏格拉底的3个弟子想找对象,曾来请教老师,问怎样找到理想的伴侣。于是苏格拉底带领弟子们来到一片麦田,让他们每人在麦田中选摘一支最大的麦穗,要求不能走回头路,且只能摘一支。

三种结局
第一位弟子刚刚走了几步便迫不及待地摘了一支麦穗,认为是最大的,结果发现后面大麦穗越来越多;第二位一直左顾右盼,东瞧西望,直到终点才发现错过了最大的麦穗;第三位把麦田分为三份,走第一个1/3时,只看不摘,分清楚大、中、小三类。在第二个1/3里验证是否正确,在第三个1/3里选择了麦穗中最大最美丽的一支。
第一位代表了社会上的闪婚一族,刚遇到一个有眼缘的,就不假思索地迅速结婚。婚后发现对方并不是自己理想的伴侣,结果很悲剧。第二位弟子属于过于挑剔型,不明白自己究竟要什么,挑来捡去挑花了眼,总觉得有更大的麦穗在后面,把合适的错过了。而最后一位心态好,明白自己要的什么样的伴侣,或许他找到的不是最漂亮的,不是最出色的,但却是最适合的。这就是爱情心理学中的“麦穗理论”Ear of wheat theory。也是管理学中的“秘书问题”
secretary problem或最优停止理论optimal stoppingtheory 。
比如要聘请一名秘书,有n人来面试,每次面试一人,面试后要当即决定是否聘用。问题是:采取什么遴选策略,使找到最适合秘书人的选几率最大?

说到秘书问题,或者麦穗理论,怎么有点像赌博。这确实属于博弈论的范畴。博弈论又称为对策论(Game Theory),既是经济学和管理学中常运用的运筹学的一个重要分支,也是现代数学中的一个分支。它的研究是建立在几率分析上的,因此可以用数学的角度来讨论这个问题。假设我们碰到的麦穗总共有n个,经过计算(计算方法略),在n/e处有个节点。节点之前有x个麦穗,节点之后有(n﹣x)个麦穗。在前x个中记住一个最大的麦穗记为a;在后(n﹣x)个中, 从x+1开始,只要大于a的,比如b,就选它了。用这样的策略来选麦穗,选中最大麦穗的几率最大。这里说的是几率,不是说选中的b一定就是全部n个麦穗中最大的,但比b更大的麦穗几率很小很小了。因而没有再必要继续浪费时间了。关键点是找到这个神秘常数e!它就是18世纪最著名的瑞士数学家欧拉研究出的自然底数e = 2.71828……。
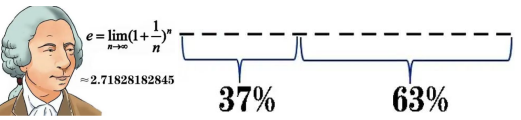
因此节点就在它的倒数1/e = 0.367879……,大约0.37处。0.37处为最优分割点,可称为37%法则.如果想摘取最大的麦穗,就应该先将前37%的麦穗作为参考,之后出现的大于前37%中最大的麦穗即可入选。37%法则,就是说最优节点是37%。在37%这个节点上,分为两段过程做出决策。两段过程:第一段37%,只看不选,但是用于确定“满意标准”;第二段63%,看到的第一个高于此“标准”者即可入选。再说一遍,37%法则并不是说一定可以选到最优,只是选到最优的几率最高的方案。即使它不是最优,距最优八九不离十。在择偶、买房等方面,37%法则都可以帮我们提供方案。有时我们可选的方案并不是很多,高于标准时就可以出手。37%是个粗略的杠杠,当可选数很少时,比如只有10个,这个节点还可以应变为40%。也就是分为前4后6两个阶段。

